Oehlschlägel-Akiyoshi, J., Malewski, P. & Mahon, J. (1999). How to define anorectic weight? Invited article in European Eating Disorders Review, 7(5), 321-333
This is a preprint of an article published in European Eating Disorders Review , 7(5), 321-333. Copyright © 1999 John Wiley & Sons, Ltd.
How to define anorectic weight?
Peter Malewski 2
Jennifer Mahon 3
Summary
Different definitions of weight criteria for the diagnosis of anorexia nervosa have been introduced, and all of them are problematic. For example, ICD-10 (World Health Organisation, 1992) suggests using 17.5 BMI instead of 85% expected weight. It is shown that any weight-for-height indices (including BMI) are inadequate corrections for body size. Furthermore BMI is not an optimum weight-for-height index, but is rather an approximation of an approximation of relative weight. Data from several countries indicate that the proportion of the population with weight below 17.5 BMI depends on age, sex and race. We suggest returning to Benn's definition of relative weight. It gives a clinically meaningful intra-individual scale, on which patients may be compared across populations. We show that BMI may be used to calculate relative weight and suggest a diagnostic criterion of 85% of median BMI from sex-, age- and country-specific tables. Such tables are already provided for German, English, French, Swedish, Italian, Japanese and (white) US populations.
Keywords: Diagnosis of anorexia nervosa, intra-individual criteria, DSM, ICD, underweight, relative weight, weight-for-height index, Benn's index, body mass index, LMS-method, robust estimation, median BMI
Introduction4
Although weight loss might seem an easy concept to define, criteria for doing so have changed with the introduction of new classification systems. In the measurement of anorexic weight, the Feighner criterion, which was adopted in DSM III (American Psychiatric Association, 1980), specified weight loss of 25% of normal body weight. The problem with this method, beyond being too restrictive, was that it relied on subjective recall of premorbid weight, which, even when accurate, was not satisfactory in those who were premorbidly obese or who had not yet reached puberty. In DSM III-R (American Psychiatric Association, 1987) this criterion was changed to 85% of expected weight; however, there was no definition of how expected weight should be judged. Most papers discussing expected weight referred to the average weight of adults given by the American insurance industry's Build and Blood Pressure Study (Society of Actuaries, 1959), which report heights and weights of insured persons in the United States. Desirable weights of adults, or the weights of insured persons in the United States associated with the lowest mortality, are also listed (Metropolitan Life Insurance Company, 1959). Like the Feighner criterion, these listings have problems. Desirable weight includes the concept of frame size, a subjective judgment. Both tables show heights measured with shoes on and weights measured wearing indoor clothing, which are potential sources of inaccuracy. Furthermore, the actuarial norms are based on a selected group of people applying for insurance in 1959 in the United States. Thus, expected weight as it is currently calculated is not reliable.
More recent authors have employed BMI rather than expected weight to evaluate nutritional status. However, this has been criticized (Brownell, 1995). Llewellyn-Jones & Abraham (1984) argued for the use of BMI in the diagnosis of anorexia nervosa. They suggested that a BMI of less than 15 in the absence of any physical or other psychiatric disorder is strongly suggestive of anorexia nervosa. In the American Psychiatric Association guidelines on eating disorders (APA, 1993) it was suggested that, due to the variety of existing standards of ideal weight, it may be preferable to use body mass index defined from tables (Hammer et al, 1991) as a standard measure of nutritional status. ICD-10 (World Health Organisation, 1992) defines a critical BMI of 17.5 for the diagnosis of anorexia nervosa. DSM-IV (APA, 1994), finally, retains the criterion of 85% of expected weight but refers to ICD's BMI criterion in a footnote.
We will show that 1) there is generally no satisfying weight-for-height correction, 2) within the limits of all possible weight-for-height corrections BMI is not optimal, 3) a BMI of 17.5 is far from being a natural constant separating underweight from normal subjects in any population. Instead of using a single BMI cut-off as the criterion for defining underweight in anorexia nervosa, we suggest keeping the definition of relative (under)weight. We show an easy way to generate the necessary normative tables and cite normative values for several populations.
Relation of body weight to height and body shape
Body weight reflects intra-individual variations in nutritional status, as for example skin-fold thickness does. It is well known, however, that directly comparing weight inter-individually across different body sizes, sexes, ages and races does not make much sense. For inter-individual comparisons of weight, physical factors affecting weight, such as height, have to be taken into consideration. Perhaps everyone knows the rule of thumb
| expected weight in kilograms = cm - 100 | (1) |
which is a special case of a linear equation
| Wkg = b * Hcm + a | (2) |
A linear relationship between weight and height such as the one above would be appropriate if a group of persons (e.g. adults) differed from another group (e.g. children) in only one dimension – height for example. However, children grow not only in height but in two other dimensions as well, and since a cube's volume is 3 times its length, there are good reasons to expect weight to be related to height in a cubic equation like
| Wkg = b * Hcm3 + a | (3) |
Such a cubic relationship between weight and height would be appropriate if people differed only in size, all having the same body shape. However, children also change their body shape when they grow up: they get longer and less compact. Thus, for average humans of any age, the 'true' relationship between weight and height is neither cubic nor linear, but somewhere in between.
Accordingly, height has been related in a quadratic way to body weight following the equation
| Wkg = b * Hcm2 + a | (4) |
or as the special case we know better
| Wkg = BMI * Hm2 | (5) |
Thus, calculating BMI as "height-corrected" body weight using the derived formula
| BMI = Wkg / Hm2 | (6) |
corresponds to some compromise5 between a linear and a cubic weight-for-height correction. Such a correction would be appropriate for a population with a particular, fixed relationship between height and body shape. In humans, however, such a relationship does not exist: healthy normal weight humans of the same height can have different body shapes, depending on sex, age, race and so on. Thus, no weight-for-height correction will be appropriate for a heterogeneous human population, simply because "height" is just a measurement of skeleton length in one dimension, where in fact 3 dimensions ought to be considered, not to mention shape differences between men and women and so on.
The limitations of corrections based exclusively on height can easily be seen by comparing correlations of weight or BMI with relative adiposity. Flegal (1990) reports correlations of weight and height-corrected BMI with the log sum of skin-fold thickness for the females (aged 18-74) in the NHANES II study: weight alone gives an r2 0.55; height-corrected BMI only improves r2 to 0.63. Obviously there remains considerable variation in weight (and BMI), which neither corresponds to height nor to obesity but rather represents varying body sizes and proportions. Not astonishingly, Chinn et. al. (1992, p. 498) conclude that "it must be recognized that neither BMI nor the weight-for-height index is a good proxy for fat mass".
Optimal weight-for-height index
Knowing that there is no really satisfying weight-for-height correction, we nevertheless enter the discussion about an "optimal" weight-for-height index. We will find that BMI is not an optimal weight-for-height index; it is, however, simple.
Benn (1971) considers two criteria of an optimal index: 1) a "good" index should be highly correlated with measures of relative adiposity (or leanness) and 2) its distribution should be independent of height. The previously cited criterion for anorexia nervosa, stipulating "85% of expected weight", is based on Benn's definition of "relative weight"
| Wrelative = Wactual / Wstandard | (7) |
as the ratio of a person's weight to a standard of weight for persons of the same height (and sex). This definition of "relative weight" has the advantage of being independent of height per definition. Benn also suggested a power-type index
| Benn's index = Wkg / Hmp | (8) |
with height raised to some power p, of which the BMI obviously is a special case with p=2. Such power-type indices are independent of height only under special circumstances. Power-type indices have been very popular because they are easy to calculate. However, it is important to note that "The power-type index described by Benn was originally intended as an approximation to this relative weight" (Flegal, 1990, p. 540). More important, various attempts to estimate an optimal p have failed:6 It has been shown that an optimal p is highly dependent on age (Fung, Lee, Lau, Chow, Wong & Davis, 1990). During some phase of childhood for both sexes the optimal p is estimated to be 3 rather than 2, and p is estimated to be higher for boys than for girls. Also the age ranges differ between the sexes: for boys p-values above 2 were estimated up to age 16, whereas for girls p-values above 2 were estimated only up to age 13. For adults the estimated p-values are less than 2, with differences across sexes and ages. For 18- to 34-year-olds, the estimate of the NHANES II data is 1.85 for males and 1.64 for females (Flegal, 1990).
Clearly there is not one single optimal p value, due to different distributions of body sizes and proportions across sexes and ages. Since p=2 is not optimal, BMI may not claim to be an optimal or even a natural power-type index. Chinn et. al. assume that "adoption of the BMI seems to have been based on a lower correlation with height and a greater correlation with skinfold thicknesses (Florey, 1970) than weight/height or weight/height3" (1992, p. 489). BMI may be considered "better" than the extremes p=1 and p=3, but not "optimal" in any sense, except that it is simple7.
Need for statistical tables
Knowing that any weight-for-height correction is insufficient and additionally knowing that BMI is not an optimal power-type weight-for-height index sheds some doubt on the utility of having a fixed BMI cut-off for anorectic weight. Obviously some non-anorectic persons could have BMI below such a cut-off and some (acute) anorectic patients can have BMI above such a cut-off. In other words: the cut-off is not clear-cut. Persons with relatively tall but slim skeletons too easily will be classified as 'anorectic', and others will not be easily enough.
However, ICD-10 promotes such a fixed cut-off. Llewellyn-Jones & Abraham (1984) also have argued for the use of an absolute BMI criterion for diagnosis of anorexia nervosa. They claim that with BMI no statistical tables are needed, so it can be used more readily. They also suggest that such a measure would be "independent of sex, age, or changing fashions in eating behaviour and possibly culture". In fact neither a "normal" BMI of 19-24.9 nor a limiting BMI of 15 (Llewellyn-Jones & Abraham, 1984) or 17.5 (ICD-10) are physiological constants. Normal and limiting BMIs vary across sexes, ages and races, so such a cut-off is not equally fair to all groups. We will show this theoretically and empirically, and it follows that statistical tables are needed.
Given our initial theoretical considerations, we know that the BMI is not invariant under transformations of body shape: snakes have a terribly low normal BMI in contrast to more compact pigs, who have a higher normal BMI. What is more, the BMI is not invariant under transformations of body size, so that elephants - as compact as pigs - have much higher normal BMI. This can easily be verified by inspecting objects of the same shape and density which differ only in size: a 1-cm cube of water has a BMI=10, a 10-cm one has a BMI=100, an 100-cm one has a BMI=1000. Larger objects have higher BMIs, so the expected BMI of a typical 'normal weight' object, despite being "corrected for height", will depend on the size and proportions of typical objects in its population. There is no such thing as a 'normal' BMI, without data about the typical and not-so-typical objects of the population. The same is true for human Davids and Goliaths, African bushmen, Swedish people and so forth.
This theoretically proven fact is of course "supported" by empirical evidence. In populations with a shorter average height or slimmer body proportions the normal BMI is also lower (for example China: Folsom, Li, Rao, Cen, Zhang, Liu, He, Irving & Dennis, 1994). Extensive German and US surveys showed sex and age differences in percentiles of BMI, partly because the ratio of muscle to fat differs (Hebebrand, Himmelmann, Heseker, Schafer & Remschmidt, 1996,Table 2 and Figure 1). In these studies, younger (smaller) people generally tend to have lower BMIs than older people, and there are differences between the sexes. Median BMI equals approximately 18 in 10-12-year-olds of both sexes but rises to approximately 24 for 48-50-year-old females and approximately 26 for 48-50-year-old males.
Therefore, it is evident that there are problems associated with using a fixed BMI criterion for the diagnosis of anorexia. Although for female adolescents aged 17-19 a BMI of 17.5 is approximately equivalent to a 15% loss in expected weight, in other age groups and in men this is not the case (Hebebrand et al., 1996; Table 1). Hebebrand et. al. (1996; Table 3) give percentages of a female German sample with a BMI lower than 17 and lower than 18 (n=11045). Linear interpolation gives a rough estimate of the percentage with BMI below 17.5 (our Table 1).
Table 1. Percentage of German female population with BMI below the criterion of 17.5, derived from Hebebrand et. al. (1996, Table 3)
| age group | 10-14 | 15-19 | 20-24 | 25-29 | 30-34 | 35-39 |
| % < BMI=17.5 | 31% | 7% | 4.4% | 3.4% | 1.9% | 1.3% |
| age group | 40-44 | 45-49 | 50-54 | 55-59 | 60-64 | 65-69 |
| % < BMI=17.5 | 0.8% | 0.9% | 0.5% | 0.6% | 0.6% | 0.6% |
Whereas in adults above the age of 40 having a BMI below 17.5 is a rather rare event (occurring in less than 1% of the population), in young adolescents especially a considerable proportion of the population has a BMI below the "anorectic" cut-off specified in ICD-10.
Even within the group of children there are complications. More detailed estimates for child populations can be derived from three European studies (Lindgren, Strandell, Cole, Healy & Tanner, 1995; Luciano, Bressan & Zoppi, 1997; White, Wilson, Greene, McCowan, Thomas, Cairns & Ricketts, 1995), which report the BMI distributions based on the Box-Cox-normalizing LMS method (Cole, 1990; Cole & Green, 1992).
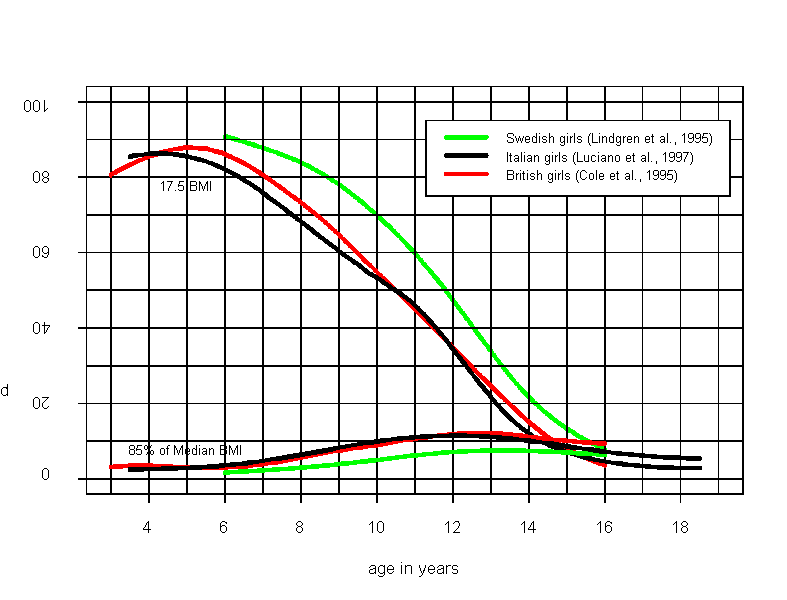
Figure 1. Percentage of girls below the ICD-10 criterion of BMI 17.5 for anorexia and below another criterion, 85% of median BMI for their age. Curves are constructed using reported LMS values from three European studies (Lindgren et al., 1995; Luciano et al., 1997; White et al., 1995).
Following Figure 1, the younger the girls, the more girls "fulfill" the ICD criterion. In 12-year-olds, where anorexia nervosa is rare, every second girl has a BMI below 17.5. The DSM-IV suggests two peaks for age of onset of anorexia nervosa, 14 and 18 years (APA, 1994, 307.1). Relating this to Figure 1 and Table 1 clearly calls the appropriateness of the ICD-criterion into question. Obviously, comparing BMI inter-individually across different sexes, ages and races raises problems similar to those found when directly comparing uncorrected weights. Thus, even when using the BMI formula, group-specific references of normality – in other words statistical tables - are needed.
Intra-individual definition of underweight
How, then, should we make use of normative data for defining abnormal weight? In the following we show that an intra-individual, relative-weight approach to using normative data is more realistic, more clinically meaningful and raises fewer technical problems than an inter-individual, extreme-values approach. Often the definition of extreme values using statistical tables relies on empirical distributions. In normally distributed samples it is common practice to define extreme values as those outside, for example, the mean +/- 3 standard deviations. More generally - when distributions are not normal - extreme percentiles are used. Following this logic to base diagnostic weight criteria for anorexia nervosa on extreme percentiles would raise problems. The current diagnostic criteria, 85% of expected weight or BMI=17.5, are fulfilled by 5 to 30 % of normal girls (cf. Table 1), depending on age. While it would be difficult to argue that 5, 10 or 30% of the population is at extreme low weight, choosing a more strict percentile criterion like the lowest 0.1% of the population would be arbitrary and would exclude real anorectic patients from diagnosis (and treatment). There is another problem with any percentage cut: The proportion of anorectic cases within a population depends on the population observed, for example, it is much higher in female than in male populations. Furthermore, there is no clinical rationale for declaring some percentage of the population "underweight". When deciding whether an individual is at an anorectic weight, it is totally irrelevant how often other people are at particular weights. The real question is an intra-individual one: Is this individual at a lower weight than she should be, to a relevant degree, say less than 85% of what would be normal for her.. Benn's definition of "relative weight" offers a way of approaching this question. It is general enough to work for more elaborated determinations of standard weight, e.g. those including body size and body proportion. As Flegal stated: "Another advantage of the relative weight approach is that it is more general than the power-type index. The predicted weights from any regression model could be used as the basis for relative weight, calculated as the ratio of actual to predicted weight" (1990, p. 545). A further advantage of "relative weight" is that only an estimate of standard weight – that is, central tendency (mean or median) – of the normative data is required rather than a complete estimation of the distribution. Thus fewer cases per group are required than would be needed for deriving reliable estimates of extreme percentiles8. This is especially important because the need for specific tables increases sample size requirements anyhow.
Robust estimate of standard weight
In order to determine relative weight, we first need to estimate standard weight. Standard weight would most naturally be addressed by very specific tables, for "all" combinations of sex, age, height, race, body proportions and so on. Particularly because there are continuous variables, such as height and age, this approach would require unrealistic sample sizes. These sizes may be reduced by employing smoothing or regression techniques. Benn's suggestion of approaching standard weight by "expected weight" via linear regression of weight on height (see equation 8) corresponds to estimating means of reference groups and assuming linear relationships across groups. However, neither estimating means nor assuming linear relationships is necessary with modern regression techniques, which allow for more robust estimates of central tendency and for modeling non-linear relationships (Hastie & Tibshirani, 1990; Rousseeuw & Leroy, 1987). The median is a simple robust measure of central tendency, which has some advantages over the arithmetic mean. It is less sensitive to outliers, requires smaller sample sizes for reasonable estimation accuracy and will be less affected by changing eating habits in parts of the population under investigation. Since medians of weight measures usually are easily available (Yanai, Kon, Kumasaka & Kawano, 1997; White et al., 1995; Rolland-Cachera, Cole, Sempe, Tichet, Rossignol, Charraud & Schulz, 1991; Luciano et al., 1997; Lindgren et al., 1995; Hebebrand et al., 1996; Hammer, Kraemer, Wilson, Ritter & Dornbusch, 1991), medians of appropriate subgroups may be used as "standard weight", as could better predictions from modern regression approaches, when available.
Integration of approaches
ICD-10 replaced the intra-individual "relative weight" criterion of 85% of premorbid weight with a fixed BMI cut-off. This may be due to a misunderstanding, since using a weight-for-height index does not require dropping the relative weight approach. Benn's original idea points towards height-specific tables, but if one uses the BMI instead (for reducing sample size requirements), relative weight (see equation 7) can still be defined as
| Wrelative-BMI = BMIactual / BMIstandard | (9) |
since BMI is a ratio-scaled measure like weight in kilograms. For practical purposes a simple and robust realization is given by using
| Westimated-relative-BMI = BMIactual / BMImedian-of-reference-group | (10) |
the median BMI of an appropriate reference group as standard weight. Figure 1 shows that the proportion of the young female population cut by the 85% median BMI criterion is generally smaller than 12% and thus its sensitivity is less affected by age than the ICD-10 criterion of 17.5 BMI. The maximum percentage of girls falling below the 85% criterion in 10-14-year-old girls reflects a greater variation of body sizes and body proportions during puberty. Table 2 summarizes median BMIs from several studies.
Table 2a: Median BMI by country, sex and age [1 =Lindgren et al. (1995),2 = smoothed medians from Luciano et al. (1997), 3=White et al. (1995),4 =Hammer et al. (1991), 5=Rolland-Cachera et al. (1991)]
| Age | Sweden1 | Italy2 | GB3 | USA (white)4 | France5 | ||||||||||
| female | male | female | male | female | male | female | male | female | male | ||||||
| 1 | 16.6 | 17.2 | |||||||||||||
| 2 | 16.0 | 16.5 | 16.2 | 16.5 | |||||||||||
| 3 | 16.2 | 16.5 | 15.6 | 16.0 | |||||||||||
| 4 | 15.8 | 16.0 | 15.8 | 16.0 | 15.4 | 15.8 | 15.4 | 15.8 | |||||||
| 5 | 15.8 | 15.9 | 15.6 | 15.7 | 15.3 | 15.5 | |||||||||
| 6 | 15.1 | 15.2 | 15.8 | 16.0 | 15.6 | 16.6 | 15.3 | 15.4 | |||||||
| 7 | 15.4 | 15.4 | 16.1 | 16.1 | 15.9 | 15.8 | 15.5 | 15.5 | |||||||
| 8 | 15.6 | 15.7 | 16.5 | 16.4 | 16.2 | 16.1 | 16.0 | 15.7 | |||||||
| 9 | 15.9 | 16.1 | 16.9 | 16.9 | 16.7 | 16.5 | 16.6 | 16.0 | |||||||
| 10 | 16.4 | 16.5 | 17.3 | 17.3 | 17.2 | 16.9 | 17.1 | 16.6 | |||||||
| 11 | 17.0 | 17.0 | 17.8 | 17.8 | 17.8 | 17.3 | 17.8 | 17.2 | |||||||
| 12 | 17.6 | 17.4 | 18.5 | 18.3 | 18.5 | 17.8 | 18.3 | 17.8 | |||||||
| 13 | 18.4 | 18.0 | 19.5 | 18.9 | 19.3 | 18.3 | 18.9 | 18.4 | |||||||
| 14 | 19.2 | 18.7 | 20.3 | 19.6 | 20.1 | 19.0 | 19.4 | 19.1 | |||||||
| 15 | 19.8 | 19.4 | 20.8 | 20.3 | 20.9 | 19.8 | 19.9 | 19.7 | 19.6 | 19.3 | |||||
| 16 | 20.4 | 20.1 | 21.1 | 21.0 | 21.6 | 20.5 | 20.2 | 20.5 | 20.2 | 19.8 | |||||
| 17 | 20.7 | 21.1 | 21.4 | 20.7 | 21.2 | ||||||||||
| 18 | 21.2 | 21.2 | 21.8 | 21.1 | 21.9 | ||||||||||
| 19 | 21.7 | 21.4 | 22.5 | ||||||||||||
| 21 | 20.5 | 21.9 | |||||||||||||
| 30 | 21.1 | 23.2 | |||||||||||||
| 40 | 22.2 | 24.4 | |||||||||||||
| 50 | 23.6 | 25.3 | |||||||||||||
| 60 | 24.4 | 25.7 | |||||||||||||
Table 2b: Median BMI by country, sex and age [1 =Hebebrand et al. (1996), 2 =Yanai et al. (1997)]
| Age | USA (white)1 | Germany1 | Japan2 | ||||||
| female | male | female | male | female | male | ||||
| 10-12 | 17.7 | 18.2 | 17.8 | 17.9 | |||||
| 13-14 | 19.1 | 19.6 | 19.1 | 19.6 | |||||
| 15-16 | 20.5 | 20.5 | 20.3 | 20.7 | |||||
| 18-19 | 23.0 | 21.6 | 22.5 | 22.1 | 20.3 | 21.5 | |||
| 20 | |||||||||
| 21-23 | 21.8 | 23.6 | 21.0 | 22.5 | |||||
| 24-26 | 22.0 | 24.2 | 21.0 | 23.1 | 20.1 | 21.6 | |||
| 27-29 | 22.1 | 24.5 | 21.3 | 23.6 | |||||
| 30-32 | |||||||||
| 33-35 | 22.9 | 25.7 | 22.0 | 24.4 | 21.0 | 23.0 | |||
| 36-38 | 23.4 | 25.8 | 22.4 | 24.9 | |||||
| 39 | |||||||||
| 40-41 | |||||||||
| 42-44 | 23.8 | 25.8 | 23.1 | 25.1 | 21.9 | 22.9 | |||
| 48-50 | 24.4 | 26.1 | 23.6 | 25.6 | |||||
| 50-59 | 22.7 | 23.1 | |||||||
| 60-69 | 22.4 | 22.5 | |||||||
Conclusion
The ICD-10 suggestion of using a critical BMI of 17.5 should not be established as a general diagnostic criterion for defining underweight in anorexia nervosa. Instead the intra-individually scaled measure of relative weight should be kept. The underweight criterion of 85% of relative weight should be used, for the sake of study comparisons, until strong evidence suggests changing it. Weight and height alone give insufficient information on obesity and undernutrition; thus any weight-for-height corrections (e.g., tables, regression, power indices) are inadequate. More research on determining standard weight is needed. The norming of body weight should account not only for sex, age and height, but also for body size and body proportions. Until adequate corrections are introduced, racial and cultural differences in distributions of body size and body proportion indicate using race- and perhaps culture-specific tables.
Since the BMI seems to be as good or as bad as optimized power-type indices, it would be reasonable first to use BMI instead of height-specific tables to reduce case requirements, and then to use median BMI as the standard weight in age-, sex- and race-specific tables.
Body weight and height are relatively easy to measure, but in light of the difficulties with norming body weight (and the obvious need for considering body proportions), other measures of nutritional status, such as skin-fold thickness, may become more attractive for use in research. If these measurements prove to be too expensive in repeated measurement designs, precise but expensive measurements could be used at the first measurement point to calculate individual standard weights. Once standard weight has been determined, subsequent inexpensive measurements of body weight would give all necessary information, if the relative weight approach were used.
References
APA. (1987). Diagnostic and statistical manual of mental disorders (DSM III-R), third edition, revised. Washington, DC: American Psychiatric Association.
APA (1993). Practice Guideline for Eating Disorders. American Journal of Psychiatry, Feb, 150(2), 212-228.
APA. (1994).Diagnostic and statistical manual of mental disorders (DSM IV), fourth edition. Washington, DC: American Psychiatric Association: .
Benn, R. T. (1971). Some mathematical properties of weight-for-height indices used as measures of adiposity. Br J Prev Soc Med, 25, 42-50.
Brownell, K. (1995). Definition and Classification of Obesity, Eating Disorders and Obesity. In B. KD & F. CG (Eds.), Eating Disorders and Obesity: A comprehensive handbook, 386-390. New York: Guilford Press.
Chinn, S., Rona, R. J., Gulliford, M. C. & Hammond, J. (1992). Weight-for-height in children aged 4-12 years. A new index compared to the normalized body mass index. Eur J Clin Nutr, 46,489-500.
Cole, T. J. (1990). The LMS method for constructing normalized growth standards. Eur J Clin Nutr, 44, 45-60.
Cole, T. J. & Green, P. J. (1992). Smoothing reference centile curves: the LMS method and penalized likelihood. Stat Med, 11, 1305-19.
Flegal, K. M. (1990). Ratio of actual to predicted weight as an alternative to a power-type weight-height index (Benn index). Am J Clin Nutr, 51, 540-7.
Florey C du V. (1970). The use and interpretation of ponderal index and other weight-height ratios in epidemiological studies. Journal Of Chronic Diseases, 23(2), 93-103.
Folsom, A. R., Li, Y., Rao, X., Cen, R., Zhang, K., Liu, X., He, L., Irving, S. & Dennis, B. H. (1994). Body mass, fat distribution and cardiovascular risk factors in a lean population of south China. J Clin Epidemiol, 47,173-81.
Frisancho, A. R. & Flegel, P. N. (1982). Relative merits of old and new indices of body mass with reference to skinfold thickness. Am J Clin Nutr, 36,697-9.
Fung, K. P., Lee, J., Lau, S. P., Chow, O. K., Wong, T. W. & Davis, D. P. (1990). Properties and clinical implications of body mass indices. Arch Dis Child, 65, 516-9.
Hammer, L. D., Kraemer, H. C., Wilson, D. M., Ritter, P. L. & Dornbusch, S. M. (1991). Standardized percentile curves of body-mass index for children and adolescents [see comments]. Am J Dis Child, 145,259-63.
Hastie, T. & Tibshirani, R. (1990). Generalized Additive Models. London: Chapman and Hall.
Hebebrand, J., Himmelmann, G. W., Heseker, H., Schafer, H. & Remschmidt, H. (1996). Use of percentiles for the body mass index in anorexia nervosa: diagnostic, epidemiological, and therapeutic considerations. Int J Eat Disord, 19, 359-69.
Lindgren, G., Strandell, A., Cole, T., Healy, M. & Tanner, J. (1995). Swedish population reference standards for height, weight and body mass index attained at 6 to 16 years (girls) or 19 years (boys). Acta Paediatr, 84,1019-28.
Llewellyn-Jones, D. & Abraham, S. F. (1984). Quetelet index in diagnosis of anorexia nervosa. Br Med J (Clin Res Ed, 288,1800.
Luciano, A., Bressan, F. & Zoppi, G. (1997). Body mass index reference curves for children aged 3-19 years from Verona, Italy. Eur J Clin Nutr, 51, 6-10.
Rolland-Cachera, M. F., Cole, T. J., Sempe, M., Tichet, J., Rossignol, C., Charraud, A. & Schulz, L. O. (1991). Body Mass Index variations: centiles from birth to 87 years. Eur J Clin Nutr, 45,13-21.
Rousseeuw, P. J. & Leroy, A. M. (1987). Robust Regression and Outlier Detection. New York: John Wiley.
White, E. M., Wilson, A. C., Greene, S. A., McCowan, C., Thomas, G. E., Cairns, A. Y. & Ricketts, I. W. (1995). Body mass index centile charts to assess fatness of British children [see comments]. Arch Dis Child, 72, 38-41.
Society of Actuaries (1959). Build and Blood Pressure Study, vol. 1. Chicago: Society of Actuaries.
Metropolitan Life Insurance Company (1959). New weight standards for men and woman. Statist Bull Metropol Life Insur Co, 40, 1-4.
World Health Organisation (1992). The ICD-10 classification of mental and behavioural disorders: clinical descriptions and diagnostic guidelines. Geneva: World Health Organisation.
Yanai, M., Kon, A., Kumasaka, K. & Kawano, K. (1997). Body mass index variations by age and sex, and prevalence of overweight in Japanese adults [In Process Citation]. Int J Obes Relat Metab Disord, 21, 484-8.
Footnotes
-
Dr. Jens Oehlschlägel-Akiyoshi (Ph.D.) is a statistical research consultant in Munich (Germany).
back to text - Peter Malewski is a research psychologist at the Medical school of Hannover, Department of Psychosomatics and Psychotherapy (Medizinische Hochschule Hannover, Abteilung Psychosomatik).
back to text - Jennifer Mahon is a research psychologist at the University of Leicester and Leicester General Hospital, Leicester, UK.
back to text - We thank Dr. Janet Treasure (Institute of Psychiatry, London), Dr. Burkard Jäger (Medizinische Hochschule Hannover), and our colleagues from Project TR-EAT at the Center for Psychotherapy Research in Stuttgart for their helpful comments.
back to text - More generally, a polynomial like kg=a+b*cm+c*cm2+d*cm3 or a natural spline could be used, but it would still be a compromise, within the limits of a simplified one-dimensional measurement of body length.
back to text - Other attempts to find formulae that give height-independent measures have been made, but these suffer from the same restriction as the power-type index. Chinn et. al. (1992) investigated variance-stabilising transformations of the form log10(Wkg+a) and find log10(Wkg-9) giving equal variances in children aged 4 to 12. Relating this to log10(Hm)*b they find b=3.7 and suggest a weight-for-height index calculated as (Wkg-9)/H3.7. They find this index height- and age-independent for ages 4 to 12, but the formula shows that the index will not work outside this range of ages. Wkg-9 is not applicable to very young children and H3.7 will give extreme values (more than cubic) for very tall persons.
back to text - Frisancho et al. find that BMI performs practically as well as Benn's index, but also conclude that "it is evident that the measures of weight and height even after being converted to other ratios cannot be used as measures of body composition. Therefore, assessments of obesity or leanness should be based on evaluations of both W/H2 and measurements of subcutaneous fat, such as skinfold thickness" (1982, p. 699).
back to text - Fitting parametric distributions may improve the estimation of extreme percentiles, but relies on assumptions and still needs more data. The LMS-Method (Cole, 1990; Cole & Green, 1992) has been popular in estimating BMI percentiles .
back to text